
Sisältö
Jotta kaksi muotoa olisi yhteneväinen, kummallakin on oltava sama määrä sivuja ja niiden kulmien on myös oltava samat. Helpoin tapa määrittää, ovatko kaksi muotoa yhteneväisiä, on kiertää yhtä muotoa, kunnes se on rivissä toisen kanssa, tai pinota muodot vain toistensa päälle nähdäksesi, ovatko jotkut päät kiinni. Jos et pysty siirtämään muotoja fyysisesti, voit käyttää kaavoja selvittääksesi, ovatko muodot yhdenmukaisia.
Kongruenttipiirit
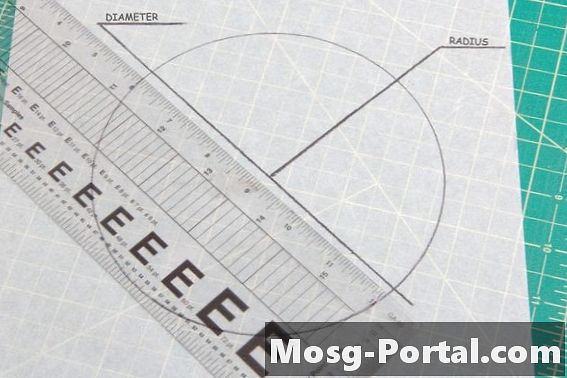
••• Ray Robert Green / Demand MediaKaikilla ympyröillä on sama 360 asteen kulma. Ainoa tekijä määritettäessä kahden ympyrän kongruenssi on verrata niiden kokoa. Halkaisija on suora viiva ympyrän keskustan läpi reunasta reunaan, kun taas ympyrän säde on pituus sen keskustasta ulkoreunaan. Kummankin mittaaminen molemmilla ympyröillä osoittaa, ovatko ne yhteneviä.
suunnikkaat
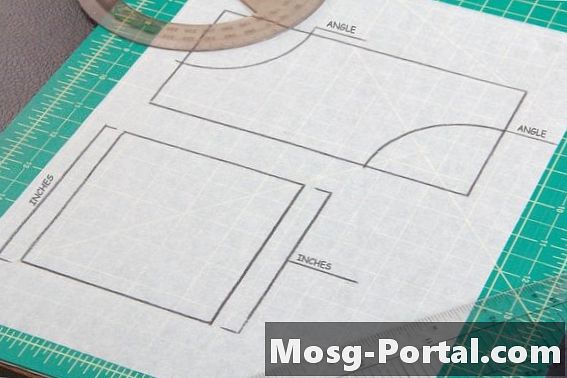
Rinnakkaiskaaviossa on kaksi paria rinnakkaisia sivuja, kuten neliöt ja suorakulmiot. Suuntaissuunnitelman vastakkaisilla sivuilla tai kulmilla on sama mitta, joten on tarpeen suorittaa kaksi kulma- tai sivumittausta suuntakuvassa, yksi jokaisesta sivuparista, jotta voidaan verrata kongruenssia toiseen muotoon.
kolmiot
••• Ray Robert Green / Demand MediaKolmioiden samanarvoisuuden löytämiseksi sinun on määritettävä jokaisen kulman tai sivun koko, koska kaikki kolme voivat olla erilaisia. On olemassa kolme postulettia, joita voidaan käyttää tunnistamaan yhdenmukaiset kolmiot. SSS-oletus on, kun mittaat kaikki kolme puolta jokaiselle kolmiolle. ASA-postulaatissa sanotaan, että jos kaksi kulmaa ja niiden liitospuoli vastaavat toisen kolmion kulmaa, niin ne ovat yhteneviä. SAS-postulaatti toimii päinvastoin ja mittaa kaksi puolta ja niiden kytkentäkulman verrattuna toiseen kolmioon.
Lauseet kongruentti kolmioille

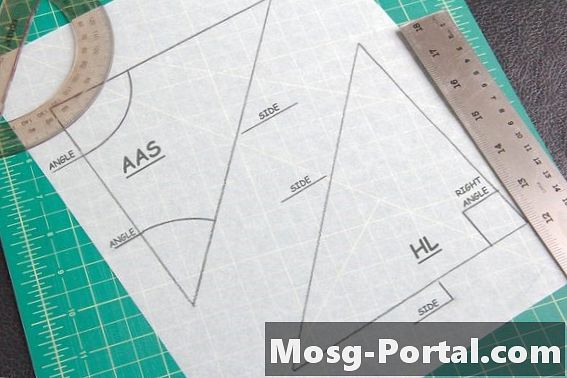
Kaksi lauseita ovat hyödyllisiä yhtenevien kolmioiden löytämiselle. AAS-lause sanoo, että jos kaksi kulmaa ja sivu, joka ei yhdistä niitä, ovat yhtä suuret kuin toisessa kolmiossa, niin ne ovat yhteneviä. Hypotenuse-Leg-lause koskee vain kolmioita, joissa on yksi 90 asteen tai "suora" kulma. Tällöin mitat hypoteenuksen - 90 asteen kulmaa vastapäätä olevan sivun - ja kolmion toisen sivun toiseen muotoon verrattuna.