Rinnakkaispiirin ominaisuudet

Sisältö

• Rinnakkaispiirikaavio
• vinkkejä
• Esimerkkejä rinnakkaispiireistä
• Rinnakkais vs. sarjan piiri
• Sarja-rinnakkaispiiri

Sähköpiirien piirielementit voivat olla järjestetty joko sarjaan tai rinnakkain. Sarjapiireissä elementit kytketään käyttämällä samaa haaraa, jonka sähkövirta kullakin on yksi kerrallaan. Rinnakkaispiireissä elementeillä on omat erilliset haaransa. Näissä piireissä virta voi kulkea eri reitteillä läpi.

Koska virta voi kulkea eri reiteillä rinnakkaispiirissä, virta ei ole vakio koko rinnakkaispiirissä. Sen sijaan haaroille, jotka on kytketty rinnakkain toisiinsa, jännite tai potentiaalin pudotus kunkin haaran yli on vakio. Tämä johtuu siitä, että virta jakaa itsensä kunkin haaran välillä määrinä, jotka ovat käänteisesti verrannollisia kunkin haaran vastukseen. Tämä aiheuttaa virran olevan suurin siellä, missä vastus on vähiten ja päinvastoin.

Nämä ominaisuudet antavat rinnakkaispiirien antaa varauksen virtata kahden tai useamman reitin läpi, mikä tekee siitä vakioehdokkaan kodeissa ja sähkölaitteissa vakaan ja tehokkaan sähköjärjestelmän kautta. Se antaa sähkön virtata piirin muiden osien läpi, kun osa on vaurioitunut tai rikki, ja ne voivat jakaa tehoa tasaisesti eri rakennusten välillä. Nämä ominaisuudet voidaan osoittaa kaavion ja esimerkin avulla rinnakkaispiiristä.

Rinnakkaispiirikaavio

vinkkejä

Esimerkkejä rinnakkaispiireistä

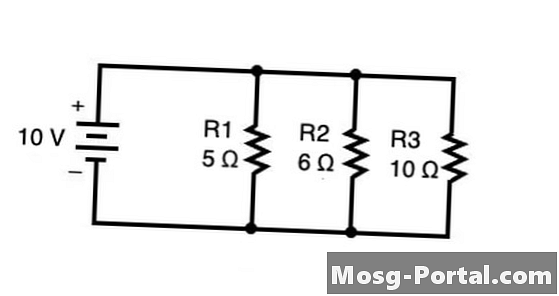
Käytä kaavaa saadaksesi toisiinsa nähden järjestettyjen vastuksien kokonaisvastus 1 / R_{kaikki yhteensä} = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn jossa jokaisen vastuksen resistanssi on summattu yhtälön oikealle puolelle. Yllä olevassa kaaviossa kokonaisvastus ohmeina (Ω) voidaan laskea seuraavasti:

Huomaa, että voit "kääntää" yhtälön molemmat puolet vaiheesta 3 vaiheeseen 4, kun yhtälön molemmilla puolilla on vain yksi termi (tässä tapauksessa 1 / R_{kaikki yhteensä} vasemmalla ja 14/30 Ω oikealla).

Kun olet laskenut resistanssin, virta ja jännite voidaan laskea ohmilain avulla V = I / R jossa V on jännite mitattuna volteina, minä on virta mitattu ampeereina, ja R on vastus ohmeissa. Rinnakkaispiireissä kunkin reitin läpi kulkevien virtojen summa on kokonaisvirta lähteestä. Virta jokaisessa piirin vastuksessa voidaan laskea kertomalla vastuksen jännite kertaa vastus. Jännite pysyy vakiona koko piirissä, joten jännite on akun tai jännitelähteen jännite.

Rinnakkais vs. sarjan piiri

••• Syed Hussain Ather

Sarjapiireissä virta on koko ajan vakio, jännitehäviöt riippuvat kunkin vastuksen resistanssista ja kokonaisvastus on kunkin vastuksen summa. Rinnakkaispiireissä jännite on koko ajan vakio, virta riippuu jokaisesta vastuksesta ja kokonaisvastuksen käänteinen on kunkin yksittäisen vastuksen käänteisen summa.

Kondensaattoreita ja induktoreita voidaan käyttää varauksen muuttamiseen sarja- ja rinnakkaispiireissä ajan myötä. Sarjapiirissä kokonaismäärä kapasitanssi piirin (annettu muuttujan C), kondensaattorin potentiaali tallentaa varausta ajan kuluessa, on kunkin yksittäisen kapasitanssin käännösten käänteinen summa ja kokonaisinduktanssi (minä), induktorien teho vapauttaa varaus ajan myötä, on kunkin induktorin summa. Sitä vastoin rinnakkaispiirissä kokonaiskapasitanssi on kunkin yksittäisen kondensaattorin summa ja kokonaisinduktanssin käänteinen on kunkin yksittäisen induktanssin käänteiden summa.

Sarja- ja rinnakkaispiireillä on myös erilaisia ​​toimintoja. Sarjapiirissä, jos yksi osa on rikki, virta ei yleensä virtaa piirin läpi. Rinnakkaispiirissä yksittäinen haaran aukko pysäyttää vain kyseisen haaran virran. Loput haarat jatkavat toimintaansa, koska virralla on useita polkuja, jotka se voi kuljettaa piirin läpi.

Sarja-rinnakkaispiiri

••• Syed Hussain Ather

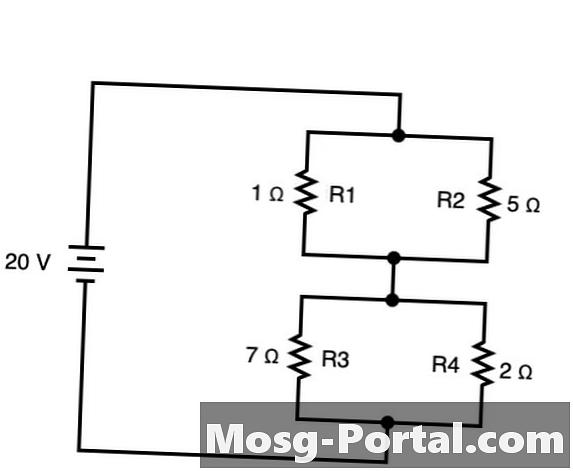
Piirit, joissa on molemmat haarautuneet elementit ja jotka on myös kytketty siten, että virta virtaa yhteen suuntaan näiden haarojen välillä molemmat sarja ja rinnakkainen. Näissä tapauksissa voit soveltaa molempien sarjojen ja rinnakkaisten sääntöjä piirille sopivalla tavalla. Yllä olevassa esimerkissä R1 ja R2 ovat rinnakkain toistensa kanssa muodostaen R5, ja niin ovat R3 ja R4 muodostamaan R6. Ne voidaan tiivistää samanaikaisesti seuraavasti:

••• Syed Hussain Ather

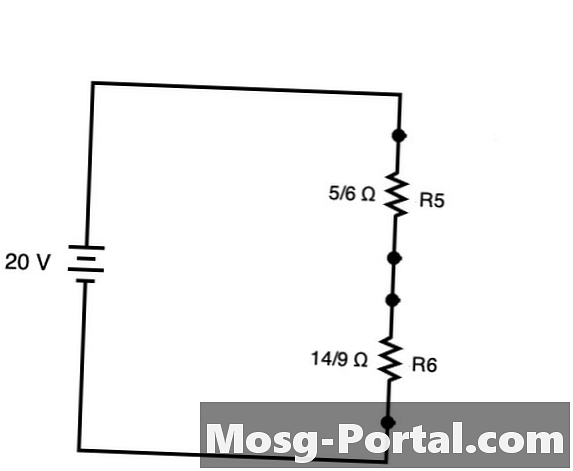
Piiriä voidaan yksinkertaistaa luomaan piiri, joka esitetään suoraan yllä R5 ja R6. Nämä kaksi vastusta voidaan lisätä suoraviivaisesti ikään kuin piiri olisi sarja.

R_{kaikki yhteensä} = 5/6 Ω + 14/9 Ω = 45/54 Ω + 84/54 Ω = 129/54 Ω = 43/18 Ω tai noin 2,38 Ω

20: n kanssa V jännitteenä Ohmin laki sanelee, että kokonaisvirta on yhtä suuri V / Rtai 20 V / (43/18 Ω) = 360/43 A tai noin 8,37 A. Tällä kokonaisvirralla voit määrittää jännitteen pudotuksen sekä R5: n että R6: n välillä Ohmin lain (V = I / R) yhtä hyvin.

varten R5, V5 = 360/43 A x 5/6 Ω = 1800/258 V tai noin 6,98 V.

varten R6, V6 = 360/43 A x 14/9 Ω = 1680/129 V tai noin 13.02 V.

Lopuksi nämä jännitteet putoavat R5 ja R6 voidaan jakaa takaisin alkuperäisiin rinnakkaisiin piireihin virran laskemiseksi R1 ja R2 varten R5 ja R2 ja R3 varten R6 käyttämällä Ohms-lakia.

I1 = (1800/258 V) / 1 = = 1800/258 A tai 6.98 A._

I2 = (1800/258 V) / 5 Ω = 1500/43 A tai yli 34,88 A._

I3 = (680/129 V) / 7 = 4760/129 A tai noin 36,90 A.

I3 = (680/129 V) / 2 Ω = 1360/129 A tai noin 10,54 A.