Sisältö
- Pituuden, leveyden, korkeuden kaava suorakaiteen muotoiselle astialle
- Sylinterin tilavuuslaskin
- Pallon tilavuus
- Pyramidin tilavuus
- Kartion tilavuus
Jos haluat laskea kolmiulotteisen hahmon tilavuuden, sinun on tiedettävä kuvion muoto. Tilavuuden laskemiseksi joidenkin lukujen mitoista on käytettävä laskentaa, mutta monille säännöllisille lukuille geometrian soveltaminen tuottaa yksinkertaisen kaavan. Muista, että kaikkien mittasuhteiden, joita käytät missä tahansa laskelmassa, on oltava samoissa yksiköissä.
Pituuden, leveyden, korkeuden kaava suorakaiteen muotoiselle astialle
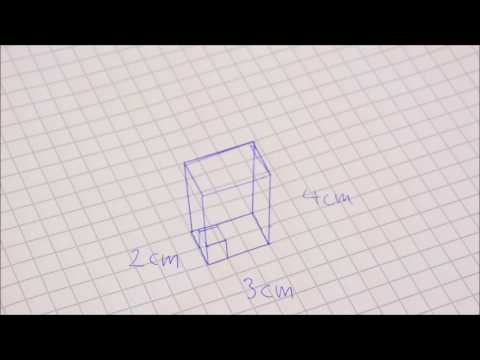
Helpoin muoto tilavuuden laskemiseksi on suorakaiteen muotoinen säiliö, kuten akvaari tai näyttelylaatikko. Sillä on kolme puolta pituutta , b ja C. Tiedät todennäköisesti jo, että voit laskea laatikon poikkileikkauksen pinta-alan kertomalla sen pituuden, leveydeltään b. Laajenna tätä aluetta nyt syvyydellä, C, ja sinulla on tilavuus:
Suorakulmion tilavuus sivuilla a, b ja c on:
Vrect = × b × C
Kuutio on erityinen suorakulmio, jolla on kaikki kolme puolta yhtä pitkät, .
Kuution tilavuus on:
Vkuutio = × × = 3
Sylinterin tilavuuslaskin
Sylinterimäisellä astialla, kuten pillerisäiliö, on pyöreä poikkileikkaus ja tietty pituus (h). Voit mitata molemmat näistä viivaimella. Ympyrän halkaisija (d) on helpompi mitata kuin säde (R), mutta kaava toimii parhaiten säteen kanssa, joten muunna vain käyttämällä kaavaa R = d/ 2. Pyöreän poikkileikkauksen pinta-ala on sitten π_r_2 tai π_d_2/ 4. Jatka kyseistä aluetta koko pituudelta (h) sylinteristä tilavuuden saamiseksi:
Vsylinteri= π × R2 × h = π × d2 / 4 × h
Pallon tilavuus
Jos mittaat pallon laajimman osan yhdeltä puolelta vastakkaiselle puolelle, saat halkaisijan, ja puolet tästä on säde (R). Voit laskea ympyrän pinnan pallojen leveimmässä pisteessä käyttämällä alakaavaa π_r_2, mutta ekstrapoloimalla tilavuuteen ei ole yksinkertaista ja se vaatii kiinteän laskennan. Onneksi sinun ei tarvitse tehdä tätä itse, koska se on jo selvitetty:
Vpallo = 4/3 × π × R3
Ellipsoidi on pitkänomainen pallo. Sen tilavuuden laskemiseksi etsi ensin keskipiste ja mittaa kolmen kohtisuoran akselin pituudet , b ja C siitä pisteestä ellipsoidin pintaan. Voit nyt laskea sen määrän:
Vellipsoidin = 4/3 × π × × b × C
Pyramidin tilavuus
Pyramidin pohjan muoto voi olla mikä tahansa monikulmio, ja on olemassa yksi yleinen kaava, jonka avulla voidaan laskea sen tilavuus:
Vpyramidi = 1/3 × b × h
missä b on pohjan ja h on korkeus.
Jos pyramidissa on kolmionmuotoinen alusta, visualisoi pohjan kallistaminen toiseen päähän. Sen kolmio, jossa pohja b ja korkeus l. Lasketaan pinta-ala kaavalla (1/2) × b × l, joten pyramidin tilavuus on:
Kolmion muotoisen pyramidin tilavuus = 1/6 × b × l × h
Jos pyramidissa on suorakaiteen muotoinen pohja l ja leveys w, pohjan pinta-ala on l × w. Pyramidin tilavuus on tällöin:
Suorakulmaisen pyramidin tilavuus = 1/3 × l × w × h
Kartion tilavuus
Kartio on muoto, jolla on pyöreä poikkileikkaus, joka kapenee pisteeseen. Jos kartion säde laajimmassa pisteessä on R ja kartion pituus h, voit löytää äänenvoimakkuuden laskemalla tai voit tehdä kuten useimmat ihmiset tekevät ja etsiä sitä.
Vkartio = 1/3 × π × R2 × h