Sisältö
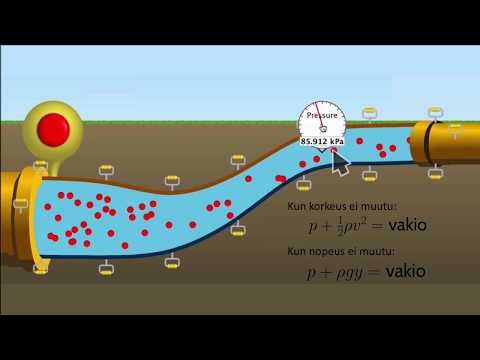
Bernoullista yhtälö antaa sinun ilmaista nesteaineiden nopeuden, paineen ja korkeuden välinen suhde virtauksen eri kohdissa. Sillä ei ole merkitystä, virtaako neste ilmakanavan kautta tai putkea pitkin liikkuvaa vettä.
Bernoulli-yhtälössä
P + 1/2 ρv2 + ρgh = C
P on paine, ρ edustaa nesteiden tiheyttä ja v on yhtä suuri kuin sen nopeus. Kirje g tarkoittaa painovoimasta johtuvaa kiihtyvyyttä ja h on nesteiden korkeus. C, vakio, antaa sinun tietää, että nesteiden staattisen paineen ja dynaamisen paineen summa kerrottuna nesteen nopeuden neliöllä on vakio kaikissa virtauksen pisteissä.
Bernoulli-yhtälöä käytetään tässä laskemaan paine ja virtausnopeus yhdessä ilmakanavan pisteessä käyttämällä paineen ja virtausnopeuden toisessa pisteessä.
Kirjoita seuraavat yhtälöt:
P1 + 1/2 ρ_v_12 + ρ_gh_1 = C
P2 + 1/2 ρ_v_22 + ρ_gh_2 = C
Ensimmäinen määrittelee nesteen virtauksen yhdessä kohdassa, jossa paine on P1, nopeus on v1, ja korkeus on h1. Toinen yhtälö määrittelee nestevirtauksen toisessa pisteessä, jossa paine on P2. Nopeus ja korkeus siinä vaiheessa ovat v2 ja h2.
Koska nämä yhtälöt ovat yhtä suuret saman vakion kanssa, ne voidaan yhdistää yhdeksi virtaus- ja paineyhtälöksi, kuten alla esitetään:
P1 + 1/2 ρv12 + ρ_gh_1 = P2 + 1/2 ρv22 + ρgh2
Poista ρgh1 ja ρgh2 yhtälön molemmilta puolilta, koska painovoiman ja korkeuden aiheuttama kiihtyvyys eivät muutu tässä esimerkissä. Virtaus- ja paineyhtälö näkyy alla esitetyllä tavalla säädön jälkeen:
P1 + 1/2 ρv12 = P2 + 1/2 ρv22
Määritä paine ja virtausnopeus. Oletetaan, että paine P1 yhdessä pisteessä on 1,2 × 105 N / m2 ja ilman nopeus tuossa pisteessä on 20 m / s. Oletetaan myös, että ilman nopeus toisessa pisteessä on 30 m / s. Ilman tiheys, ρ, on 1,2 kg / m3.
Järjestä yhtälö ratkaistavaksi P: lle2, tuntematon paine, ja virtaus- ja paineyhtälö näkyvät kuvassa:
P2 = P1 − 1/2 ρ(v22 − v12)
Korvaa muuttujat todellisilla arvoilla saadaksesi seuraava yhtälö:
P2 = 1.2 × 105 N / m2 − 1/2 × 1,2 kg / m3 × (900 m2/ s2 - 400 m2/ s2)
Yksinkertaista yhtälö saadaksesi seuraavan:
P2 = 1.2 × 105 N / m2 − 300 kg / m / s2
Koska 1 N on 1 kg / m / s2, päivitä kaava alla esitetyllä tavalla:
P2 = 1.2 × 105 N / m2 − 300 N / m2
Ratkaise yhtälö P2 saada 1,197 × 105 N / m2.