Sisältö
Korkeus on kiinteä ulottuvuus objektin määrän määrittämisessä. Objektin korkeusmittauksen löytämiseksi sinun on tiedettävä sen geometrinen muoto, kuten kuutio, suorakulmio tai pyramidi. Yksi helpoimmista tavoista ajatella korkeutta, koska se vastaa tilavuutta, on ajatella muita mittoja perusalana. Korkeus on vain niin monta pohja-alaa pinottu toisiinsa. Yksittäiset objektimäärän kaavat voidaan järjestää uudelleen korkeuden laskemiseksi. Matemaatikot ovat jo kauan sitten laatineet kaikkien tunnettujen geometristen muotojen tilavuuskaavat. Joissakin tapauksissa, kuten kuutiossa, korkeuden ratkaiseminen on helppoa; toisissa se vie vähän yksinkertaisen algebran.
Suorakulmaisten esineiden korkeus
Kiinteän suorakaiteen tilavuuden kaava on leveys x syvyys x korkeus. Jaa tilavuus pituuden ja leveyden tuloksella suorakulmaisen esineen korkeuden laskemiseksi. Tässä esimerkissä suorakaiteen muotoisen esineen pituus on 20, leveys 10 ja tilavuus 6000. 20: n ja 10: n tulo on 200, ja 6 000 jaettuna 200: lla saadaan luvulla 30. Kohteen korkeus on 30.
Kuution korkeus
Kuutio on eräänlainen suorakulmio, jossa kaikki sivut ovat samat. Joten löytääksesi tilavuus, kuutio minkä tahansa sivun pituus. Laske kuution tilavuuden kuutiojuuri saadaksesi korkeus. Tässä esimerkissä kuution tilavuus on 27. 27: n kuutiojuuri on 3. Kuution korkeus on 3.
Sylinterin korkeus
Sylinteri on suora sauvan tai tapin muotoinen, pyöreä poikkileikkaus, jolla on sama säde ylhäältä alas. Sen tilavuus on ympyrän pinta-ala (pi x säde ^ 2) kertaa korkeus. Jaa sylinterin tilavuus säteen neliöllä kerrottuna pi: llä sen korkeuden laskemiseksi. Tässä esimerkissä sylinterin tilavuus on 300 ja säde on 3. Squaring 3 johtaa 9: ään, ja kertomalla 9 pi: llä, saadaan 28,274. 300: n jakaminen 28,274: lla johtaa tulokseen 10,61. Sylinterin korkeus on 10,61.
Pyramidin korkeus
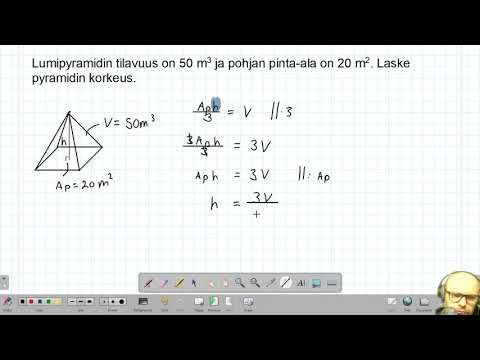
Neliön muotoisessa pyramidissa on tasainen neliöpohja ja neljä kolmionmuotoista sivua, jotka kohtaavat yläosassa olevaan pisteeseen. Tilavuuskaava on pituus x leveys x korkeus ÷ 3. Kolminkertaista pyramidin tilavuus ja jaa sitten tämä määrä alustan pinta-alalta sen korkeuden laskemiseksi. Tässä esimerkissä pyramidin tilavuus on 200 ja sen pohjan pinta-ala on 30. Kertomalla 200: lla 3 saadaan 600: lla ja jakamalla 600: lla 30: ta tuloksella 20. Pyramidin korkeus on 20.
Prisman korkeus
Geometria kuvaa muutamaa erityyppistä prismaa: joissakin on suorakaiteen muotoisia, toisissa kolmion muotoisia pohjia. Kummassakin tapauksessa poikkileikkaus on sama läpi sylinterin. Prisman tilavuus on pohjan pinta-ala kertaa korkeus. Joten korkeuden laskemiseksi jaa prisman tilavuus sen ala-alasta. Tässä esimerkissä prisman tilavuus on 500 ja sen pohjapinta-ala on 50. Jakamalla 500 50: llä saadaan luvulla 10. Prisman korkeus on 10.