Kuinka laskea kulmanopeus

Sisältö

• Liikkeen perusteet
• Kulmanopeuden yhtälö
• Pyörivät liikeyhtälöt
• Liittyvät määrät ja ilmaisut
• Kulmanopeus vs. lineaarinen nopeus

Arjen keskusteluissa "nopeutta" ja "nopeutta" käytetään usein vuorottelevasti. Fysiikassa näillä termeillä on kuitenkin erityisiä ja selkeitä merkityksiä. "Nopeus" on esineen siirtymänopeus avaruudessa, ja se annetaan vain määrällä tiettyjä yksiköitä (usein metreinä sekunnissa tai mailia tunnissa). Nopeus puolestaan ​​on suuntaan kytketty nopeus. Nopeutta sitten kutsutaan skalaarimäärään, kun taas nopeus on vektorimäärää.

Kun auto vetoketjuu moottoritietä pitkin tai baseball kiisee ilman läpi, näiden esineiden nopeus mitataan suhteessa maahan, kun taas nopeuteen sisältyy enemmän tietoa. Esimerkiksi, jos olet autossa, joka kulkee nopeudella 70 mailia tunnissa Interstate 95: llä Yhdysvaltojen itärannikolla, on myös hyödyllistä tietää, kulkeeko auto koilliseen kohti Bostonia vai etelään kohti Floridaa. Baseballin kanssa kannattaa ehkä tietää, muuttuuko sen y-koordinaatti nopeammin kuin sen x-koordinaatti (lentopallo) vai onko käänteinen totta (linja-asema). Entä renkaiden kehruu tai baseballin pyöriminen (spin), kun auto ja pallo siirtyvät lopulliseen määränpäähänsä? Tällaisille kysymyksille fysiikka tarjoaa käsitteen kulmanopeus.

Liikkeen perusteet

Asiat liikkuvat kolmiulotteisen fyysisen tilan läpi kahdella pääasiallisella tavalla: kääntäminen ja kierto. Käännös on koko esineen siirtyminen paikasta toiseen, kuten auto, joka ajaa New Yorkista Los Angelesiin. Pyöritys puolestaan ​​on esineen syklinen liike kiinteän pisteen ympäri. Monilla esineillä, kuten yllä olevassa esimerkissä, löytyy molemmat liiketyypit samanaikaisesti; kun lentopallo liikkui ilman läpi kotilevystä kohti ulkoreuna-aitaa, se pyörii myös tietyllä nopeudella oman keskipisteensä ympäri.

Näiden kahden liiketyypin kuvaaminen käsitellään erillisinä fysiikkaongelmina; ts. laskettaessa etäisyyttä, jonka pallo kulkee ilman läpi, perustuen esimerkiksi sen alkuperäiseen laukaisukulmaan ja nopeuteen, jolla se lähtee lepakosta, voit jättää huomiotta sen pyörimisen, ja kun lasket sen pyörimistä, voit pitää sitä yhdessä istuvana paikka nykyisiin tarkoituksiin.

Kulmanopeuden yhtälö

Ensinnäkin, kun puhut "kulmasta" mistä tahansa, oli kyse sitten nopeudesta tai muusta fyysisestä suuresta, ymmärrä, että koska olet tekemisissä kulmien kanssa, puhut ympyrässä tai sen osissa matkustamisesta. Voit muistuttaa geometriasta tai trigonometriasta, että ympyrän kehä on sen halkaisija ja vakiopi pi, tai πd. (Pi: n arvo on noin 3.14159.) Tämä ilmaistaan ​​yleisemmin ympyrän säteen perusteella R, joka on puolet halkaisijasta, mikä tekee kehästä 2πr.

Lisäksi olet todennäköisesti oppinut jonnekin matkan varrella, että ympyrä koostuu 360 asteesta (360 °). Jos siirrät etäisyyttä S ympyrää pitkin, kulmasiirto θ on yhtä suuri kuin S / r. Yksi täysi kierros antaa sitten 2πr / r, joka vain jättää 2π. Tämä tarkoittaa sitä, että kulmat, jotka ovat alle 360 ​​°, voidaan ilmaista pi: na tai toisin sanoen radiaaneina.

Kun kaikki nämä tiedot kerätään yhteen, voit ilmaista ympyrän kulmia tai osia muissa yksiköissä kuin asteissa:

360 ° = (2π) radiaani tai

1 radiaani = (360 ° / 2π) = 57,3 °,

Kun lineaarinen nopeus ilmaistaan ​​pituutena yksikköaikaa kohti, kulmanopeus mitataan radiaaneina aikayksikköä kohti, yleensä sekunnissa.

Jos tiedät, että hiukkanen liikkuu pyöreällä polulla nopeudella v matkan päästä R ympyrän keskustasta suuntaan v aina ollessa kohtisuorassa ympyrän säteen kanssa, kulmanopeus voidaan kirjoittaa

ω = v / r,

missä ω on kreikkalainen omega-kirjain. Kulmanopeuden yksiköt ovat radiaaneja sekunnissa; voit myös pitää tätä yksikköä "vastavuoroisina sekunteina", koska v / r antaa m / s jaettuna m: llä, tai s^-1, eli radiaanit ovat teknisesti yksikkömäärätön.

Pyörivät liikeyhtälöt

Kulmakiihtyvyyskaava johdetaan samalla olennaisella tavalla kuin kulmanopeuden kaava: Se on yksinkertaisesti lineaarinen kiihtyvyys ympyrän säteen nähden kohtisuorassa suunnassa (vastaavasti sen kiihtyvyys ympäri ympyrän reittiä koskevassa tangentissa missä tahansa pisteessä) jaettuna ympyrän tai ympyrän osan säteellä, joka on:

a = a_T/ R

Tämän antaa myös:

α = ω / t

koska ympyräliikkeessä, a_T = ωr / t = v / t.

α, kuten luultavasti tiedät, on kreikan kirjain "alfa". Alaindeksi "t" tarkoittaa tässä "tangenttia".

Kummallista kyllä, kiertoliike ylpeilee muun tyyppisellä kiihtyvyydellä, jota kutsutaan centripetaaliseksi ("keskipisteenhaku") kiihtyväksi. Tämän antaa lauseke:

_C = v²/ R

Tämä kiihtyvyys on suunnattu kohti pistettä, jonka ympäri kyseinen esine pyörii. Tämä voi tuntua oudolta, koska esine ei ole lähemmäs tätä keskipistettä säteen jälkeen R on korjattu. Ajattele keskikohdan kiihtyvyyttä vapaana pudotuksena, jossa esineellä ei ole vaaraa iskeytyä maahan, koska esinettä kohti sitä vetävä voima (yleensä painovoima) kompensoidaan tarkasti tangentiaalisella (lineaarisella) kiihtyvyydellä, joka kuvataan ensimmäisessä yhtälössä Tämä alue. Jos _C eivät olleet yhtä kuin _T, esine joko lentää avaruuteen tai törmää pian ympyrän keskelle.

Liittyvät määrät ja ilmaisut

Vaikka kulmanopeus ilmaistaan ​​yleensä, kuten todettiin, radiaaneina sekunnissa, voi olla tapauksia, joissa on edullista tai välttämätöntä käyttää astetta sekunnissa, tai päinvastoin, muuntaa asteista radiaaneiksi ennen ongelman ratkaisemista.

Sano, että sinulle kerrottiin, että valonlähde pyörii 90 ° joka sekunti vakionopeudella. Mikä on sen kulmanopeus radiaaneissa?

Muista ensin, että 2π radiaani = 360 °, ja aseta suhde:

360 / 2π = 90 / x

360x = 180π

x = ω = π / 2

Vastaus on puoli pi radiaania sekunnissa.

Jos sinulle kertoisi edelleen, että valonsäteen etäisyys on 10 metriä, mikä olisi säteiden kärjen lineaarinen nopeus v, sen kulmakiihtyvyys α ja sen centripetaalinen kiihtyvyys _C?

Ratkaista varten v, ylhäältä, v = ωr, missä ω = π / 2 ja r = 10m:

(π / 2) (10) = 5π rad / s = 15,7 m / s

Ratkaista varten α, lisää vain toinen aikayksikkö nimittäjään:

a = 5π rad / s²

(Huomaa, että tämä toimii vain ongelmissa, joissa kulmanopeus on vakio.)

Lopuksi, myös ylhäältä, a_C = v²/ r = (15,7)²/ 10 = 24,65 m / s².

Kulmanopeus vs. lineaarinen nopeus

Edelliseen ongelmaan perustuen kuvittele itsesi erittäin suurelle merimatkalle, jolla on epätodennäköinen 10 kilometrin (10 000 metrin) säde. Tämä merirosvo tekee yhden täydellisen kierroksen minuutin välein ja 40 sekunnin välein tai 100 sekunnin välein.

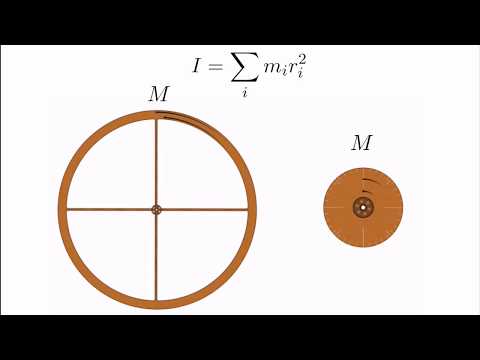
Yksi seuraus kulmanopeuden, joka ei ole riippuvainen etäisyydestä pyörimisakselista, ja lineaarisen ympyränopeuden, joka ei ole, välisestä erotuksesta on, että kaksi ihmistä kokee saman ω voi olla kokenut huomattavasti erilaisia ​​fyysisiä kokemuksia. Jos satut olemaan 1 metrin päässä keskustasta, jos tämä oletettu, massiivinen merirosvo, sinun lineaarinen (tangentiaalinen) nopeutesi on:

ωr = (2π rad / 100 s) (1 m) = 0,0628 m / s tai 6,29 cm (alle 3 tuumaa) sekunnissa.

Mutta jos olet tämän hirviön kehällä, lineaarinen nopeutesi on:

ωr = (2π rad / 100 s) (10 000 m) = 628 m / s. Se on noin 1 406 mailia tunnissa, nopeampi kuin luoti. Odota!