Kuinka laskea sähkövaraus

Sisältö

• Sähkölatauskaava
• Sähkövaraus ja painovoima: yhtäläisyydet
• Sähkön varauksen säilyminen
• Laskettujen elektronien lukumäärä
• Piirien sähkövarauksen laskeminen
• Sähkökentän kaava
• Universumin nettovaraus
• Sähkövirran laskeminen latauksella
• Lataus ja staattinen sähkö
• Sähköjohtimet
• Gausss-laki muissa tilanteissa

Olipa kyse staattisesta sähköstä, jonka karvainen takki luovuttaa, tai televisioihin kytkettävästä sähköstä, voit oppia lisää sähkövarauksesta ymmärtämällä taustalla olevan fysiikan. Latauslaskentatavat riippuvat sähkön luonteesta, kuten periaatteet siitä, kuinka varaus jakaa itsensä esineiden kautta. Nämä periaatteet ovat samat riippumatta siitä, missä olet maailmankaikkeudessa, joten sähkövaraus on tieteen perusominaisuus.

Sähkölatauskaava

Laskemiseen on monia tapoja sähkövaraus erilaisille haitoille fysiikassa ja sähkötekniikassa.

Coulombs-laki käytetään yleensä laskettaessa sähkövarauksella kulkevien hiukkasten aiheuttamaa voimaa, ja se on yksi yleisimmistä käyttämistäsi sähkövarausyhtälöistä. Elektronien yksittäiset varaukset ovat -1602 × 10^-19 coulombs (C), ja protoneissa on sama määrä, mutta positiivisessa suunnassa, 1,602 × 10 ⁻¹⁹ C. Kaksi maksua q₁ ja q₂ _et erotetaan etäisyydellä _r, voit laskea sähkövoiman F_E tuotettu käyttämällä Coulombs-lakia:

F_E = frac {kq_1q_2} {r ^ 2}

jossa K on vakio K = 9.0 × 10 ⁹ nm² / C². Fyysikot ja insinöörit käyttävät joskus muuttujaa e viitata elektronin varaukseen.

Huomaa, että vastakkaisten merkkien (plus ja miinus) varauksissa voima on negatiivinen ja siten houkutteleva näiden kahden varauksen välillä. Kahdelle saman merkin lataukselle (plus ja plus tai miinus ja miinus) voima on vastenmielinen. Mitä suurempia varaukset ovat, sitä voimakkaampi niiden välillä on houkutteleva tai vastenmielinen voima.

Sähkövaraus ja painovoima: yhtäläisyydet

Coulombs-laki on uskomattoman samanlainen kuin Newtonin laki painovoiman suhteen F_{G ​} = G m₁m₂ / R² painovoima F_G, joukot m₁ja m₂, ja painovoimavakio G = 6.674 × 10 ⁻¹¹ m³/ kg s². Ne molemmat mittaavat erilaisia ​​voimia, vaihtelevat suuremman massan tai varauksen mukaan ja riippuvat molempien esineiden välisestä sädestä toiseen voimaan. Yhdenmukaisuuksista huolimatta on tärkeätä muistaa, että gravitaatiovoimat ovat aina houkuttelevia, kun taas sähkövoimat voivat olla houkuttelevia tai heijastuttavia.

Sinun tulisi myös huomata, että sähkövoima on yleensä paljon voimakkaampi kuin painovoima, joka perustuu lakien vakioiden eksponentiaalivoiman eroihin. Näiden kahden lain väliset yhtäläisyydet osoittavat paremmin symmetriaa ja malleja universumin yleisten lakien keskuudessa.

Sähkön varauksen säilyminen

Jos järjestelmä pysyy eristettynä (ts. Ilman kosketusta mihinkään muuhun sen ulkopuolella), se säästää varausta. Maksun säilyttäminen tarkoittaa, että sähkövarauksen kokonaismäärä (positiivinen varaus miinus negatiivinen varaus) pysyy samana järjestelmälle. Latauksen säilyttäminen antaa fyysikoille ja insinöörille mahdollisuuden laskea kuinka paljon varaus siirtyy järjestelmien ja niiden ympäristön välillä.

Tämän periaatteen ansiosta tutkijat ja insinöörit voivat luoda Faraday-häkejä, joissa käytetään metallisia suojauksia tai pinnoitteita estääkseen varauksen pääsyn. Faraday-häkeissä tai Faraday-suojaissa käytetään sähkökenttiä, jotka pyrkivät jakamaan varauksia materiaaliin uudelleen, jotta kentän vaikutus voidaan poistaa ja estää latauksia vahingoittamasta tai pääsemästä sisätiloihin. Niitä käytetään lääketieteellisissä laitteissa, kuten magneettikuvauslaitteissa tietojen vääristymisen estämiseksi, ja vaarallisissa ympäristöissä työskentelevien sähkömiesten ja linja-autojen suojavälineissä.

Voit laskea tilavuuden nettovarausvirran laskemalla syötetyn varauksen kokonaismäärä ja vähentämällä jäljellä olevan varauksen kokonaismäärä. Varattujen elektronien ja protonien kautta voidaan luoda tai tuhota varautuneita hiukkasia tasapainottuakseen varauksen säilyvyyden mukaan.

Laskettujen elektronien lukumäärä

Tietäen, että elektronin varaus on -1602 × 10 ⁻¹⁹ C, varaus -8 × 10 ⁻¹⁸ C koostuisi 50 elektronista. Voit löytää tämän jakamalla sähkövarauksen määrän yhden elektronin varauksen suuruudella.

Piirien sähkövarauksen laskeminen

Jos tiedät sähkövirta, sähkövarauksen virtaus esineen läpi, joka kulkee piirin läpi ja kuinka kauan virtaa käytetään, voit laskea sähkövarauksen virran yhtälöllä Q = Se jossa Q on koululoissa mitattu kokonaisvaraus, minä on virta ampeereina, ja T on aika, jonka virta syötetään sekunneissa. Voit myös käyttää Ohmin lakia (V = IR) jännitteen ja vastusvirran laskemiseksi.

Piirille, jonka jännite on 3 V ja vastus 5 Ω, jota käytetään 10 sekunnin ajan, vastaava tulokseksi saatava virta on minä = V / R = 3 V / 5 Ω = 0,6 A, ja kokonaisvaraus olisi Q = se = 0,6 A × 10 s = 6 C.

Jos tiedät mahdollisen eron (V) piirissä ja työssä käytettyinä volteinaW) jouleina, jotka tehdään sen soveltamisjakson aikana, varaus coulombsissa, Q = W / V.

Sähkökentän kaava

••• Syed Hussain Ather

Sähkökenttä, sähkövoima yksikköä kohti, leviää säteittäisesti ulos positiivisista varauksista negatiivisiin varauksiin ja voidaan laskea seuraavilla: E = F_E / q, jossa F_E on sähkövoima ja q on varaus, joka tuottaa sähkökentän. Koska peruskenttä ja voima ovat laskelmissa sähkön ja magneettisuuden suhteen, sähkövaraus voidaan määritellä aineen ominaisuudeksi, joka aiheuttaa hiukkaselle voiman sähkökentän läsnä ollessa.

Vaikka esineen nettovaraus tai kokonaisvaraus olisi nolla, sähkökentät mahdollistavat varausten jakautumisen eri tavoin esineiden sisällä. Jos niiden sisällä on varajakautumisia, joiden tulokseksi ei ole nolla nettovarausta, nämä esineet ovat polarisoitunut, ja varaus, jonka nämä polarisaatiot aiheuttavat, tunnetaan nimellä sidotut maksut.

Universumin nettovaraus

Vaikka tutkijat eivät ole yhtä mieltä siitä, mikä maailmankaikkeuden kokonaisvaraus on, he ovat tehneet koulutettuja arvauksia ja testanneet hypoteeseja eri menetelmillä. Voit huomata, että painovoima on maailmankaikkeuden hallitseva voima kosmologisessa mittakaavassa, ja koska sähkömagneettinen voima on paljon voimakkaampi kuin painovoima, jos universumilla oli nettovaraus (joko positiivinen tai negatiivinen), niin sinun on kyettävä nähdä todisteita siitä niin suurilla etäisyyksillä. Tämän todisteen puuttuminen on saanut tutkijat uskomaan, että maailmankaikkeus on varausneutraali.

Keskusteluissa ovat myös kysymykset siitä, onko maailmankaikkeus aina ollut varausneutraalia tai miten maailmankaikkeuden varaus on muuttunut ison iskun jälkeen. Jos maailmankaikkeudella olisi nettovaraus, silloin tutkijoiden tulisi pystyä mittaamaan taipumuksensa ja vaikutuksensa kaikkiin sähkökenttälinjoihin siten, että positiivisten varausten negatiivisista varauksista yhdistämisen sijaan ne eivät koskaan lopu. Tämän havainnon puuttuminen viittaa myös väitteeseen, jonka mukaan maailmankaikkeudella ei ole nettovarausta.

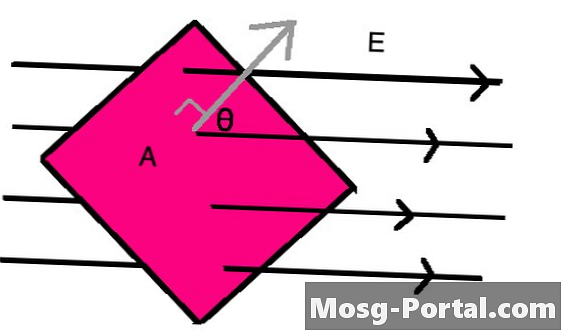
Sähkövirran laskeminen latauksella

••• Syed Hussain Ather

sähkövirta tasomaisen (ts. tasaisen) alueen läpi sähkökentän E on kenttä kerrottuna kentän kanssa kohtisuoran alueen komponentilla. Saadaksesi tämän kohtisuoran komponentin, käytät kentän ja mielenkiintoisen tason välisen kulman kosinusta kosmetiikan kaavassa, jota edustaa Φ = EA cos (θ), missä θ on alueeseen kohtisuoran viivan ja sähkökentän suunnan välinen kulma.

Tämä yhtälö, joka tunnetaan nimellä Gausss-laki, kertoo myös, että näiden kaltaisille pinnoille, joita kutsut Gaussin pinnat, kaikki nettovaraukset olisivat sen tason pinnalla, koska sähkökenttä olisi tarpeen luoda.

Koska tämä riippuu vuon laskemisessa käytetyn pinta-alan geometriasta, se vaihtelee muodon mukaan. Pyöreä alue, vuotava alue olisi π_r_² kanssa R ympyrän säteenä, tai sylinterin kaarevalle pinnalle vuon pinta-ala olisi ch jossa C on pyöreän sylinterin pinnan kehä ja h on sylinterien korkeus.

Lataus ja staattinen sähkö

Staattinen sähkö syntyy, kun kaksi esinettä eivät ole sähköisessä tasapainossa (tai sähköstaattinen tasapaino), tai että on olemassa nettovarausvirta objektista toiseen. Kun materiaalit hankaavat toisiaan vastaan, ne siirtävät latauksia toistensa välillä. Suujen hankaaminen matolla tai paisuneen ilmapallojen kumi hiuksillasi voi tuottaa näitä sähkömuotoja. Shokki siirtää nämä ylimääräiset kulut takaisin tasapainotilan palauttamiseksi.

Sähköjohtimet

Varten a kapellimestari (materiaali, joka siirtää sähköä) sähköstaattisessa tasapainossa, sähkökentän sisällä on nolla ja sen pinnan nettovarauksen on pysyttävä staattisessa tasapainossa. Tämä johtuu siitä, että jos kenttää olisi, johtimessa olevat elektronit jakautuvat uudelleen tai kohdistuvat uudelleen vastauksena kenttään. Tällä tavalla ne peruuttavat kaikki kentät heti, kun ne luodaan.

Alumiini ja kuparilanka ovat yleisiä johdinmateriaaleja, joita käytetään virtojen siirtämiseen, ja usein käytetään myös ionijohteita, jotka ovat ratkaisuja, joissa käytetään vapaasti kelluvia ioneja, jotta varaus virtaa helposti läpi. Puolijohteet, kuten sirut, joiden avulla tietokoneet voivat toimia, käyttävät myös vapaasti kiertäviä elektroneja, mutta ei niin monta kuin johtimet. Puolijohteet, kuten pii ja germanium, vaativat myös enemmän energiaa varauksen kiertämiseksi ja yleensä niiden johtavuus on matala. Sitä vastoin, eristeet kuten puu, älä anna varauksen virtata helposti niiden läpi.

Koska kenttää ei ole sisällä, Gaussin pinnalla, joka sijaitsee juuri johtimen pinnan sisällä, kentän on oltava nolla kaikkialla, jotta vuoto on nolla. Tämä tarkoittaa, että johtimen sisällä ei ole nettovarausta. Tästä voidaan päätellä, että symmetrisille geometrisille rakenteille, kuten palloille, varaus jakautuu tasaisesti Gaussin pinnan pinnalle.

Gausss-laki muissa tilanteissa

Koska pinnan nettovarauksen on pysyttävä staattisessa tasapainossa, minkä tahansa sähkökentän on oltava kohtisuorassa johtimen pintaan, jotta materiaali voi siirtää varauksia. Gaasss-laki antaa sinun laskea tämän sähkökentän suuruuden ja johtimen virtauksen. Johtimen sisällä olevan sähkökentän on oltava nolla, ja ulkopuolelta sen tulee olla kohtisuora pintaan nähden.

Tämä tarkoittaa, että lieriömäisellä johtimella, jonka kenttä säteilee seinistä kohtisuorassa kulmassa, kokonaisvirta on yksinkertaisesti 2_E__πr_² sähkökenttään E ja R lieriömäisen johtimen pyöreän pinnan säde. Voit myös kuvata pinnan nettovarauksen käyttämällä σ, varaustiheys pinta-alayksikköä kohti kerrottuna pinta-alalla.