Sisältö
Geometriassa kahdeksankulmainen on monikulmio, jolla on kahdeksan sivua. Säännöllisessä kahdeksankulmassa on kahdeksan yhtä suurta puolta ja yhtä suuret kulmat. Säännöllinen kahdeksankulma tunnistetaan yleisesti pysäytysmerkeistä. Oktaedri on kahdeksan puolinen monihalkaisija. Tavallisessa oktaedrissa on kahdeksan kolmiota, joiden reunat ovat yhtä pitkät. Se on käytännössä kaksi neliömäistä pyramidia, jotka kokoontuvat tukikohtaansa.
Kahdeksankulmainen aluekaava
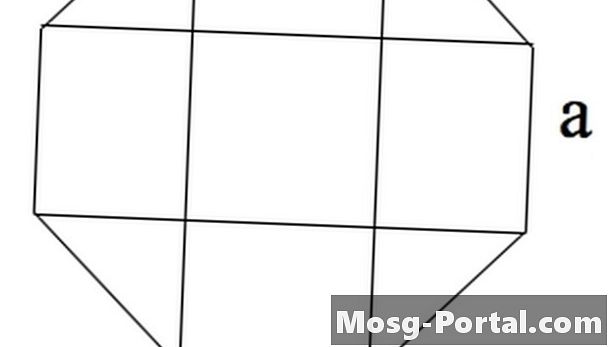
Kaava säännöllisen kahdeksankulman alueelle, jonka sivut ovat pituudeltaan "a", on 2 (1 + sqrt (2)) a ^ 2, jossa "sqrt" ilmaisee neliöjuuren.
Johtaminen
Kahdeksankulmaista voidaan pitää 4 suorakulmiona, yksi neliö keskellä ja neljä tasakulmaista kolmiota nurkissa.
Neliö on pinta-alaa ^ 2.
Kolmioilla on sivut a, a / sqrt (2) ja a / sqrt (2) Pythagoran lauseen mukaan. Siksi jokaisella on pinta-ala ^ 2/4.
Suorakulmioiden pinta-ala on a * a / sqrt (2).
Näiden 9 alueen summa on 2a ^ 2 (1 + sqrt (2)).
Oktaedronimäärän kaava
Sivujen "a" säännöllisen oktaedron tilavuuden kaava on ^ 3 * sqrt (2) / 3.
Johtaminen
Nelipuolisen pyramidin pinta-ala on pohjan * korkeus / 3. Pinta-alan normaalin kahdeksankulman pinta-ala on 2 * perus * korkeus / 3.
Pohja = a ^ 2 triviaalia.
Valitse kaksi vierekkäistä kärkeä, sano "F" ja "C." "O" on keskellä. FOC on tasakulmainen suorakulmainen kolmio, jonka kanta on "a", joten OC: n ja OF: n pituus on a / sqrt (2) Pythagoran lauseen perusteella. Joten korkeus = a / sqrt (2).
Joten normaalin oktaedron tilavuus on 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Pinta-ala
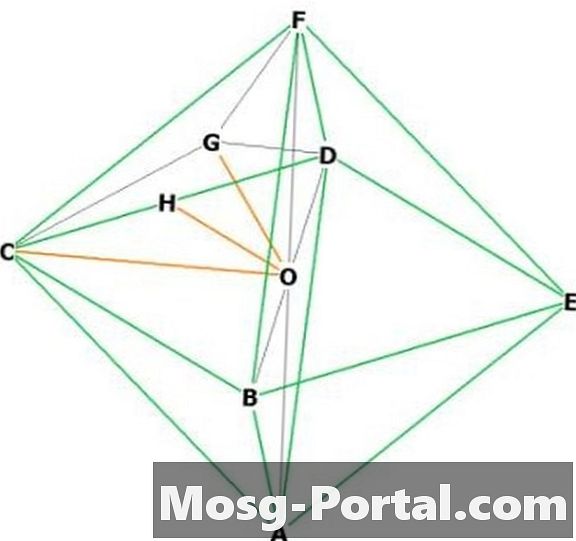
Säännöllinen oktaedrien pinta on tasasivuisen kolmion pinta, jonka sivu "a" on 8 kertaa.
Pythagora-lauseen käyttämiseksi pudota viiva kärjestä pohjaan. Tämä luo kaksi suoraa kolmiota, joiden hypotenuse on pituus "a" ja yhden sivun pituus "a / 2". Siksi kolmannen sivun on oltava sqrt = sqrt (3) a / 2. Joten tasasivuisen kolmion pinta-ala on korkeus * pohja / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
8 sivulla normaalin oktaedron pinta-ala on 2 * sqrt (3) * a ^ 2.