Sisältö
Hihnapyörillä voidaan perustaa useita mielenkiintoisia tilanteita, joilla testataan opiskelijoiden ymmärtäminen Newtonin toisesta liikelaista, energian säilyttämislaista ja fysiikan työn määritelmästä. Yksi erityisen opettavainen tilanne löytyy ns. Differentiaalipyörästä, joka on yleinen työkalu, jota käytetään mekaanikkokaupoissa raskaiden nostojen tekemiseen.
Mekaaninen etu
Kuten vivulla, voiman kohdistamisen etäisyyden lisääminen verrattuna kuorman nostoetäisyyteen lisää mekaanista etua tai vipuvaikutusta. Oletetaan, että käytetään kahta hihnapyörien lohkoa. Yksi kiinnittyy kuormaan; Yksi kiinnittyy yllä olevaan tukeen. Jos taakkaa on tarkoitus nostaa X-yksikköä, myös alemman hihnapyörän tulee nousta X-yksikköä. Yllä oleva hihnapyörä ei liiku ylös tai alas. Siksi kahden hihnapyörän välisen etäisyyden on lyhennettävä X yksikköä. Kahden hihnapyörän väliin silmukoitujen linjojen pituuksien on kummankin lyhennettävä X-yksikköä. Jos Y on tällaisia linjoja, vetäjän on vetävä X --- Y-yksiköitä nostaaksesi kuorma X-yksiköitä. Joten vaadittava voima on 1 / Y kertaa kuorman paino. Mekaanisen edun sanotaan olevan Y: 1.
Energian säästölaki
Tämä vipuvaikutus on seurausta energiansäästölaista. Muista, että työ on eräänlaista energiaa. Työn alla tarkoitamme fysiikan määritelmää: voima, joka kohdistuu kuormituksen väliseen etäisyyteen, jota kohti kuorma liikkuu voimalla. Joten jos kuorma on Z Newtonia, X-yksiköiden nostamiseen tarvittavan energian on oltava yhtä suuri kuin vetäjän tekemä työ. Toisin sanoen Z --- X: n on oltava yhtä suuri (vetäjän kohdistama voima) --- XY. Siksi vetäjän kohdistama voima on Z / Y.
Tasauspyörä
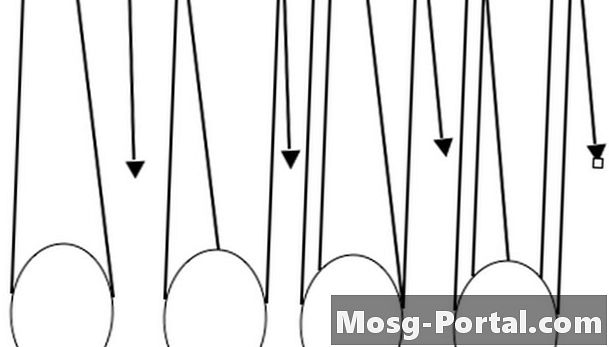
Mielenkiintoinen yhtälö syntyy, kun teet linjasta jatkuvan silmukan, ja tuesta roikkuvassa lohkossa on kaksi hihnapyörää, toinen hieman pienempi kuin toinen. Oletetaan myös, että lohkon kaksi hihnapyörää on kiinnitetty siten, että ne pyörivät yhdessä. Kutsu hihnapyörien säteet "R" ja "r", missä R> r.
Jos vetolaite vetää tarpeeksi viivaa kiinteiden hihnapyörien kiertämiseksi yhden kierroksen läpi, hän on vetänyt ulos 2πR viivaa. Suurempi hihnapyörä on sitten ottanut 2πR viivaa kuorman tukemisesta. Pienempi hihnapyörä on kiertynyt samaan suuntaan, päästäen 2πr linjaa ulos kuormaan. Joten kuorma nousee 2πR-2πr. Mekaaninen etu on vetämä etäisyys jaettuna nostetulla etäisyydellä, tai 2πR / (2πR-2πr) = R / (R-r). Huomaa, että jos säteet eroavat vain 2 prosentilla, mekaaninen etu on mahtava 50: 1.
Tällaista hihnapyörää kutsutaan differentiaalipyöriksi. Se on yleinen kiinnike autokorjaamoissa. Sillä on mielenkiintoinen ominaisuus, että vedin, jonka vetin vetää, voi ripustaa löysästi, kun taakkaa pidetään korkealla, koska kitkaa on aina niin paljon, että kahden hihnapyörän vastakkaiset voimat estävät sitä kääntymästä.
Newtonin toinen laki


Oletetaan, että kaksi lohkoa on kytketty, ja yksi, nimeltään M1, ripustaa hihnapyörän. Kuinka nopeasti ne kiihtyvät? Newtonin toinen laki liittyy voimaan ja kiihtyvyyteen: F = ma. Kahden lohkon massa tunnetaan (M1 + M2). Kiihtyvyyttä ei tunneta. Voima tunnetaan M1: n painovoiman vetämisestä: F = ma = M1 --- g, missä g on painovoimakiihtyvyys maan pinnalla.
Muista, että M1 ja M2 kiihdytetään yhdessä. Niiden kiihtyvyyden a löytäminen on nyt vain korvaamisen kysymys kaavaan F = ma: M1 --- g = (M1 + M2) a. Tietenkin, jos kitka M2: n ja pöydän välillä on yksi voimista, joita F = M1 --- g on vastustettava, niin tämä voima lisätään helposti myös yhtälön oikealle puolelle, ennen kiihtyvyyttä, a ratkaistu
Lisää ripustettavia lohkoja

Entä jos molemmat lohkot riippuvat? Sitten yhtälön vasemmalla puolella on kaksi lisäystä yhden sijaan. Kevyempi kulkee syntyvän voiman vastakkaiseen suuntaan, koska suurempi massa määrää kaksimassasysteemin suunnan; sen vuoksi pienemmän massan painovoima olisi vähennettävä. Oletetaan M2> M1. Sitten yllä oleva vasen puoli muuttuu M1 --- g: stä M2 --- g-M1 --- g: ksi. Oikea käsi pysyy samana: (M1 + M2) a. Kiihtyvyys, a, ratkaistaan sitten triviaalisesti aritmeettisesti.