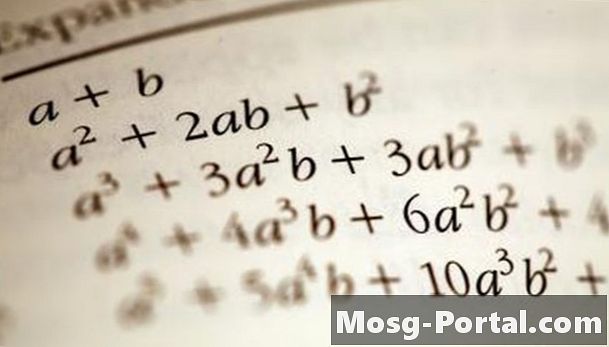
Sisältö
Polynomin tai trinomian faktointi tarkoittaa sitä, että ilmaista se tuotteena. Polynomien ja trinomiaalien tekijäkerroin on tärkeä, kun ratkaistaan nollia. Faktoritoiminta ei vain helpota ratkaisun löytämistä, vaan koska nämä lausekkeet sisältävät eksponentteja, ratkaisuja voi olla useita. Polynomien ja trinomien faktorointiin on useita lähestymistapoja, ja käytetty lähestymistapa vaihtelee. Näihin menetelmiin sisältyy suurimman yhteisen tekijän löytäminen, factoring ryhmittelyllä ja FOIL-menetelmä.
Suurin yhteinen tekijä
Etsi mikä tahansa polynomi- tai trinomiarvo faktoroimalla suurin yhteinen tekijä, jos sellainen on. Yleensä nopein tapa tehdä tämä on alfaktorisointi - toisin sanoen alkulukujen käyttäminen numeron ilmaisemiseksi tuotteena. Joissakin polynomeissa suurin yhteinen tekijä voi sisältää myös muuttujan.
Tarkastellaan lukuja 20 ja 30. 20: n peruskerroin on 2 x 2 x 5 ja 30: n peruskerroin on 2 x 3 x 5. Yleiset kertoimet ovat kaksi ja viisi. Kaksi kertaa viisi on yhtä suuri kuin 10, joten 10 on suurin yhteinen tekijä.
Tarkista kertoimen tulos kertomalla. Voit laskea lausekkeen 7x ^ 2 + 14 - 7 (x ^ 2 + 2). Kun tämä tekijä kerrotaan, se palaa alkuperäiseen lausekkeeseen, 7x ^ 2 + 14, joten se on oikein.
ryhmittymä
Faktoroi tietyt polynomit neljällä termällä käyttämällä ryhmittelyä.
Tarkastellaan polynomia x ^ 3 + x ^ 2 + 2x + 2, jossa ei ole muuta tekijää kuin yksi, joka on yhteinen kaikille termeille.
Kertoimet x ^ 3 + x ^ 2 ja 2x + 2 erikseen: x ^ 3 + x ^ 2 = x ^ 2 (x + 1) ja 2x + 2 = 2 (x + 1). Siksi x ^ 3 + x ^ 2 + 2x + 2 = x ^ 2 (x + 1) + 2 (x + 1) = (x ^ 2 + 2) (x + 1). Viimeisessä vaiheessa huomioit x + 1, koska se on yleinen tekijä.
FOIL-menetelmä
Tyypin ax ^ 2 + bx + c tekijätrinomit FOIL - ensimmäinen, ulkoinen, sisäinen, viimeinen - menetelmällä. Faktoitu trinomi koostuu kahdesta binomista. Esimerkiksi lauseke (x + 2) (x + 5) = x ^ 2 + 5x + 2x + 2 (5) = x ^ 2 + 7x + 10. Kun johtava kerroin a on yksi, kerroin, b on binomiaalien vakiotermien summa - tässä tapauksessa kaksi ja viisi - ja trinomin vakiotermi c on näiden termien tuote.
Kerro suurin yhteinen tekijä, jos sellainen on. Etsi kaksi tekijää a: sta, luettelo kaikista mahdollisista tekijöistä ennen jatkamista, jos a ei ole yksi tai alkuluku. Kerro kukin numero x: lla. Nämä ovat kunkin binomiaalin ensimmäinen termi. Monissa trinomiokertoimissa kerroin a on yhtä. Tarkastellaan esimerkkiä 3x ^ 2 - 10x - 8. Ei ole yhteistä tekijää, ja ensimmäisten ehtojen ainoat mahdollisuudet ovat 3x ja x. Tämä tarjoaa binomiaalien ensimmäiset ehdot: (3x +) (X +).
Löydä binomiaalien viimeiset termit kertomalla niin, että löydät luvun, joka on yhtä suuri kuin c. Edellä olevaa esimerkkiä käyttämällä viimeisillä ehdoilla tulisi olla -8. -8: lle on olemassa useita tekijöitä, mukaan lukien 8 ja -1 ja 2 ja -4. Tee luettelo kaikista mahdollisista tekijöistä ennen jatkamista.
Etsi ulkoisista ja sisäisistä tuotteista, jotka johtuvat yllä olevista vaiheista, joiden summa on bx. Testaa edellisessä vaiheessa löydettyjä tekijöitä kokeiluilla ja virheillä. Tarkista vastaus kertomalla FOIL-menetelmällä. (3x + 2) (x - 4) = 3x ^ 2 - 12x + 2x - 8 = 3x ^ 2 - 10x - 8